Approaches to developing progression for teaching computing

25 February 2020

A progression framework is the backbone of any subject curriculum. It denotes the sequence in which children learn, noting where core understanding of a topic is established in order to progress. Through our work developing a bank of teaching resources that deliver the computing curriculum in England, as part of the National Centre for Computing Education, we’ve studied a lot of progression frameworks, examination specifications, and even some research papers. From our research, we have found that there are two quite different ways of presenting progression that show what should be taught and when it should be taught, as well as information on how or why concepts should be taught.

Firstly, there is the approach of creating a categorisation of skills and concepts into a list or table. Sequencing is shown by having objectives listed by Key Stage, year group, or even by learners’ age. Examples of this approach include the CAS computing progression pathways, and the Massachusetts Digital Literacy and Computer Science Curriculum Framework. They are essentially a list of required knowledge, bundled by theme.

Another approach is to use a map of possible trajectories through learning waypoints and importantly how they connect to each other. This approach is able to highlight where prerequisite knowledge needs to be mastered before students can move on, as well as the dependent knowledge contained in other nodes that need to be mastered in order to progress. Cambridge Mathematics are leading the way in “developing a flexible and interconnected digital framework to help reimagine mathematics education 3-19”. We’ve been lucky enough to learn from their work which has helped us create the learning graphs.

We organised computing content (concepts, knowledge, skills, and objectives) into interconnected networks we call learning graphs. We found that nodes often form clusters, corresponding to specific themes, and we could connect them if they represent two adjacent waypoints in the learning process. Depending on the level of abstraction, the nodes in a learning graph could contain anything ranging from the contents of a curriculum strand across an entire Key Stage, to the learning objectives of a six-lesson unit. Initially, the graphs we produce are in a ‘fluid’ state: they uncover the structure of the content and the possible journeys through it, without being bound to a specific teaching pathway. The graphs eventually reach a ‘solid’ state, where the nodes are further structured and arranged to reflect our suggestions on the order that the content could actually be delivered.

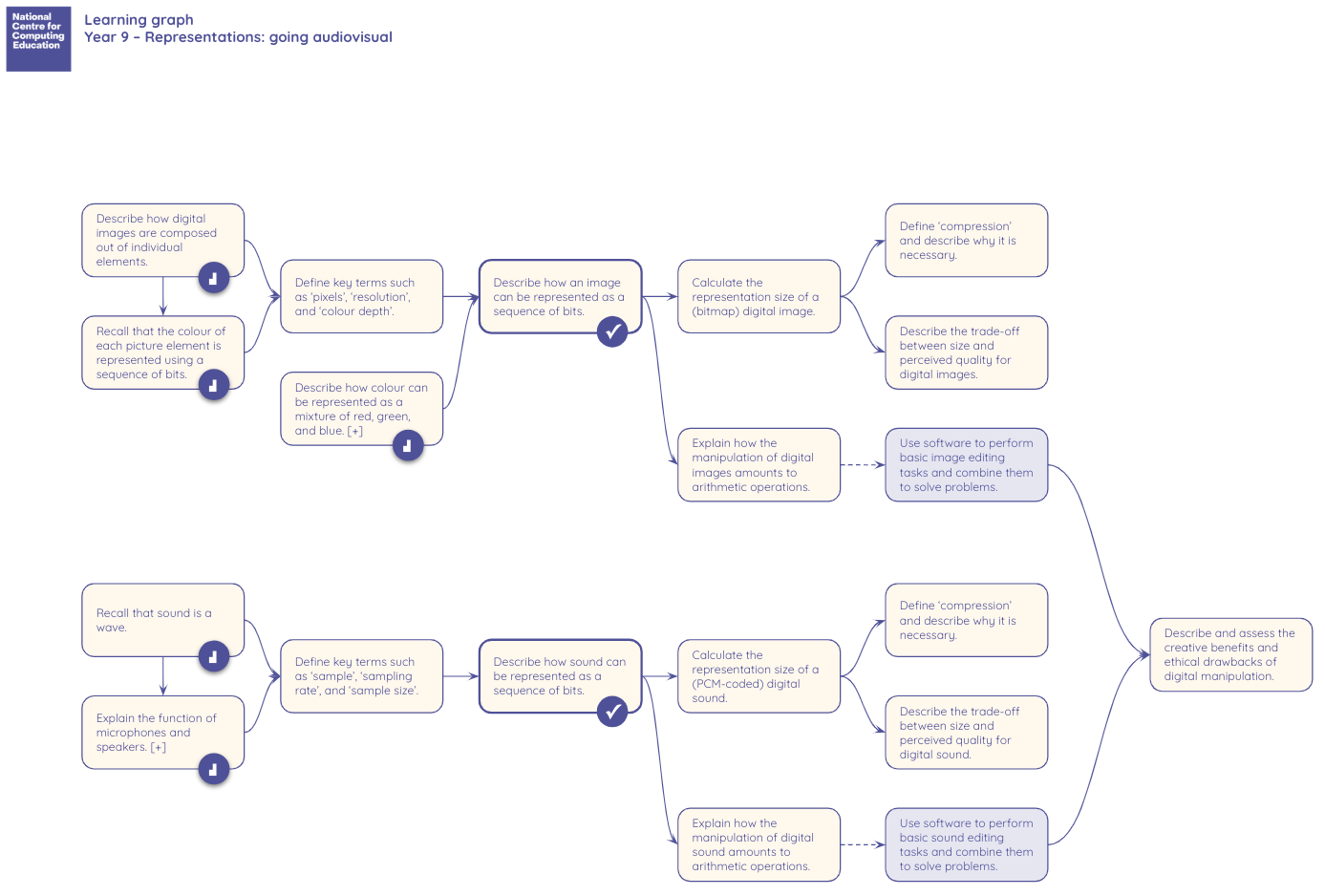
We believe that learning graphs are useful to teachers on a whole new level. They directly inform lesson planning, but also add value by showing opportunities to assess understanding at landmark waypoints in a lesson or unit. By checking that students are grasping the concepts, teachers are able to think more about how they are teaching and can revisit knowledge that perhaps didn’t land with learners the first time.

All progression frameworks are subjective, and with little research into computing education we rely on teachers’ experience of combining the ‘what’ we teach and ‘how’ to teach it in order to help inform this work.

Read more

  • Cambridge Mathematics. An update on the Cambridge Mathematics Framework. Retrieved January 2020 from: www.cambridgemaths.org/Images/cambridge-mathematics-framework.pdf
  • Binkowski, T.A., Franklin, D., Rich, K.M., Strickland, C. (2018) Decomposition: A K-8 Computational Thinking Learning Trajectory. In: Proceedings of the 2018 ACM Conference on International Computing Education Research (ICER ’18), pp. 124–132.
  • Clements, D., and Sarama, J. (2004) Learning trajectories in mathematics education. Mathematical Thinking and Learning. 6 (2), 81-89.  
  • Confrey, J., Edgington, C., Holt Wilson, P., Sztajn, P. (2012) Learning trajectory based instruction: toward a theory of teaching.Educational Researcher 41 (5), 147-156.

Call to action

About the author

Carrie Anne Philbin, Director of Educator Support, Raspberry Pi Foundation